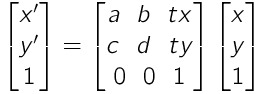アフィン変換とは?
状態:-
閲覧数:1,917
投稿日:2014-05-14
更新日:2016-09-12
「線型変換(回転、拡大縮小、剪断)」と「平行移動」を組み合わせた変換
・線形変換に平行移動を加えたものをアフィン変換と呼ぶ
※ 線形変換は平行移動を表すことができないため
具体的には?
・画像の拡大縮小、回転、平行移動などをまとめて、3×3の行列を使って変換する
アフィン (affine) とは?
・ラテン語で「類似・関連」を意味する affinis に由来する言葉
線形変換とは?
・「変換の前に直線だった場所は、変換後も直線のまま保たれる」変換のこと
・直線は変換によって曲がったりしない
・さらに、「直線上に点A,B,Cが並んでいたとき、変換の前後でAB:BCの比が変化しない」
・線の形が変わらないから線形変換という
・線形変換に平行移動を加えたものをアフィン変換と呼ぶ
※ 線形変換は平行移動を表すことができないため
具体的には?
・画像の拡大縮小、回転、平行移動などをまとめて、3×3の行列を使って変換する
アフィン (affine) とは?
・ラテン語で「類似・関連」を意味する affinis に由来する言葉
線形変換とは?
・「変換の前に直線だった場所は、変換後も直線のまま保たれる」変換のこと
・直線は変換によって曲がったりしない
・さらに、「直線上に点A,B,Cが並んでいたとき、変換の前後でAB:BCの比が変化しない」
・線の形が変わらないから線形変換という
幾何学的変換
概要
デジタルオブジェクトは画素の集合だから、画素1つ1つに対して処理を行えば、平行移動、拡大・縮小、回転させることは可能
・画素の位置 … (x, y)
平行移動
計算式
・tx … x方向への移動量
・ty … y方向への移動量
・全画素分下記計算を繰り返せば、オブジェクトの平行移動が可能
x' = x + tx
y' = y + ty
・上記計算式は行列を用いることで1つにまとめることが可能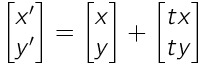
拡大・縮小
計算式
・sx … x方向への拡大
・sy … y方向への拡大量
・全画素分下記計算を繰り返せば、オブジェクトの拡大・縮小が可能
x' = sx × x
y' = sy × y
・上記計算式は行列を用いることで1つにまとめることが可能
・拡大縮小行列
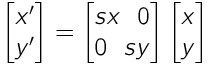
回転
計算式
・θ … 回転する角度
・sin … 三角関数のサイン
・cos … 三角関数のコサイン
・全画素分下記計算を繰り返せば、オブジェクトの回転が可能
(変換後の x 座標) = (変換前の x 座標)×cosθ - (変換前の y 座標)×sinθ
x' = xcosθ - ysinθ
(変換後の y 座標) = (変換前の x 座標)×sinθ + (変換前の y 座標)×cosθ
y' = xsinθ + ycosθ
・上記計算式は行列を用いることで1つにまとめることが可能・拡大縮小行列
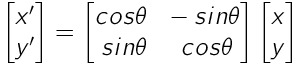
【極座標とは】
・平面上の点を,原点からの距離rと始線(x軸の正の向き)からの偏角θの組(r, θ)で表したもの
・原点からの距離(r)と偏角(θ)からなる座標のこと
・「距離と角度」で表される座標
・平面上の1点を極と定め、その点から半直線を一本引く
・この半直線を始線と定め、平面上の点を(点から極までの距離,点と極を結んだ直線と始線がなす角度ラジアン)という方法で表した(r,θ)
・極は原点、始線はx軸の正の側、角度はy軸の正の向きに向かった動径、とそれぞれ同一視
アフィン変換 計算式
汎用的
・計算式をひとつにして汎用的に使用できるようにする
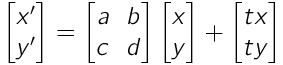
アフィン行列
・3次元の座標を導入して、1つの行列の乗算にまとめる
・この行列を用いることで、任意の線形変換(拡大・縮小・回転など)と平行移動を組み合わせた変換ができるようになる
・これがアフィン変換